📐 AMO-Bench: Large Language Models Still
Struggle in High School Math Competitions

Shengnan An*♢, Xunliang Cai♢, Xuezhi Cao*♢, Xiaoyu Li♢, Yehao Lin♢, Junlin Liu†♣,
Xinxuan Lv♢, Dan Ma♢, Xuanlin Wang†♡, Ziwen Wang♢, Shuang Zhou♢
(Alphabetical order by last name)
Meituan LongCat Team
*Correspondence to: anshengnan@meituan.com, caoxuezhi@meituan.com.
♢Meituan
♣University of Chinese Academy of Sciences
♡Harbin Institute of Technology
†Work done during the internship at Meituan.
📃 Paper Code 🤗 Dataset 🏆 Leaderboard

🏆Leaderboard🏆

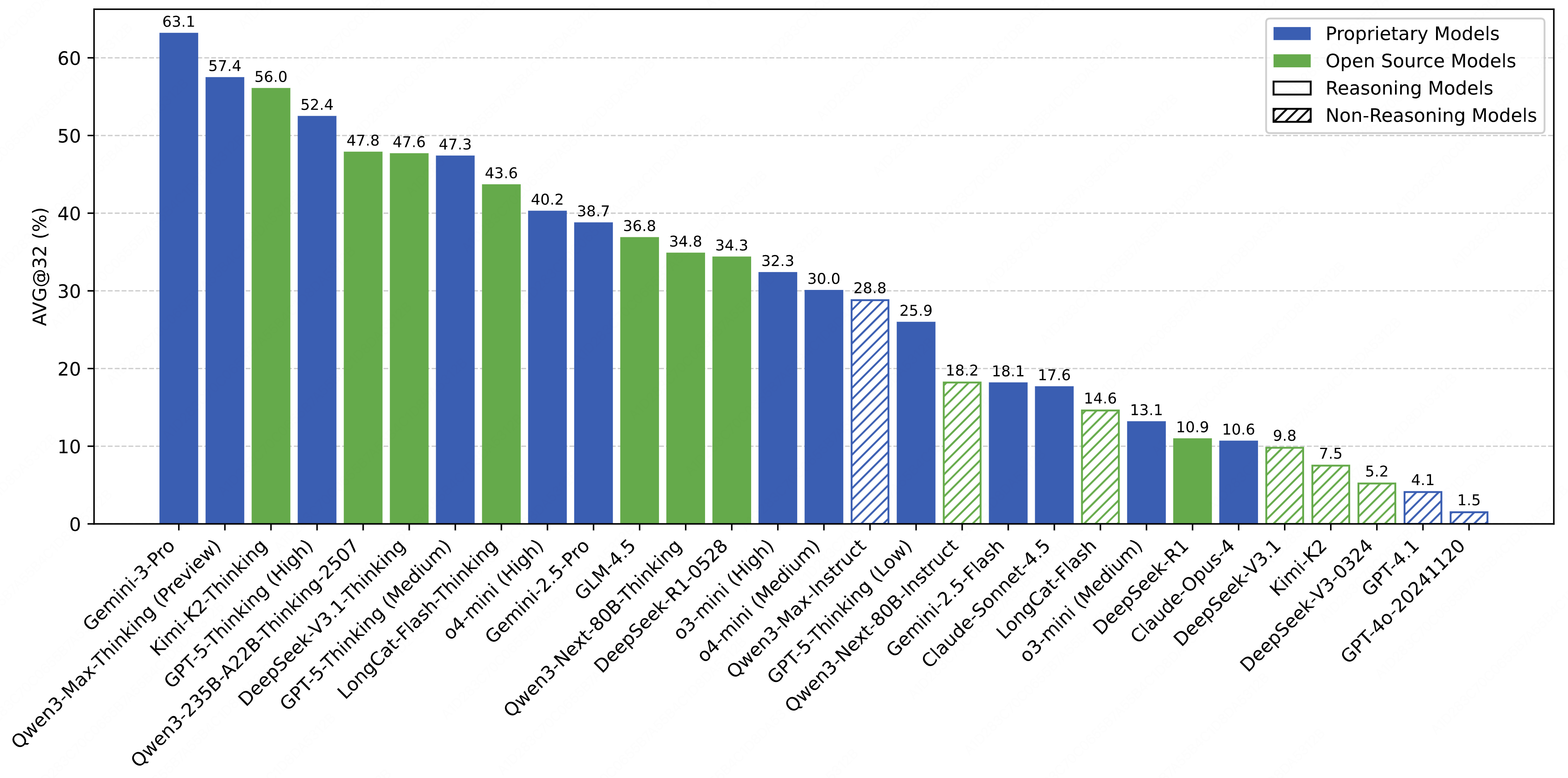
Sizes of model trees

Updates:
- 2025.12.01: We have added Token Efficiency showing the number of output tokens used by models in the leaderboard. Gemini 3 Pro achieves the highest token efficiency among top-performance models!
- 2025.11.24: Gemini 3 Pro achieves 63.1%, setting a new SOTA and breaking 60% for the first time! We have updated the Leaderboard with the results of Gemini 3 Pro and Qwen3-Max-Thinking (Preview).
- 2025.11.19: Kimi-K2-Thinking achieves 56.0%, new SOTA on Leaderboard!
- 2025.11.05: The problem statement of **Problem 35** has been revised in 🤗 Huggingface Dataset: (1) the five integers that sum to $k$ should be **non-negative** rather than positive, and (2) we also stipulate that 1 couldn't be replaced with five integers. Additionally, for the strictly positive case in the original problem statement, the correct answer should be 7656 (see this discussion for details). Thanks to the feedback from @applesilicon!
- 2025.10.31: We release the dataset, evaluation code, and technical report of AMO-Bench.

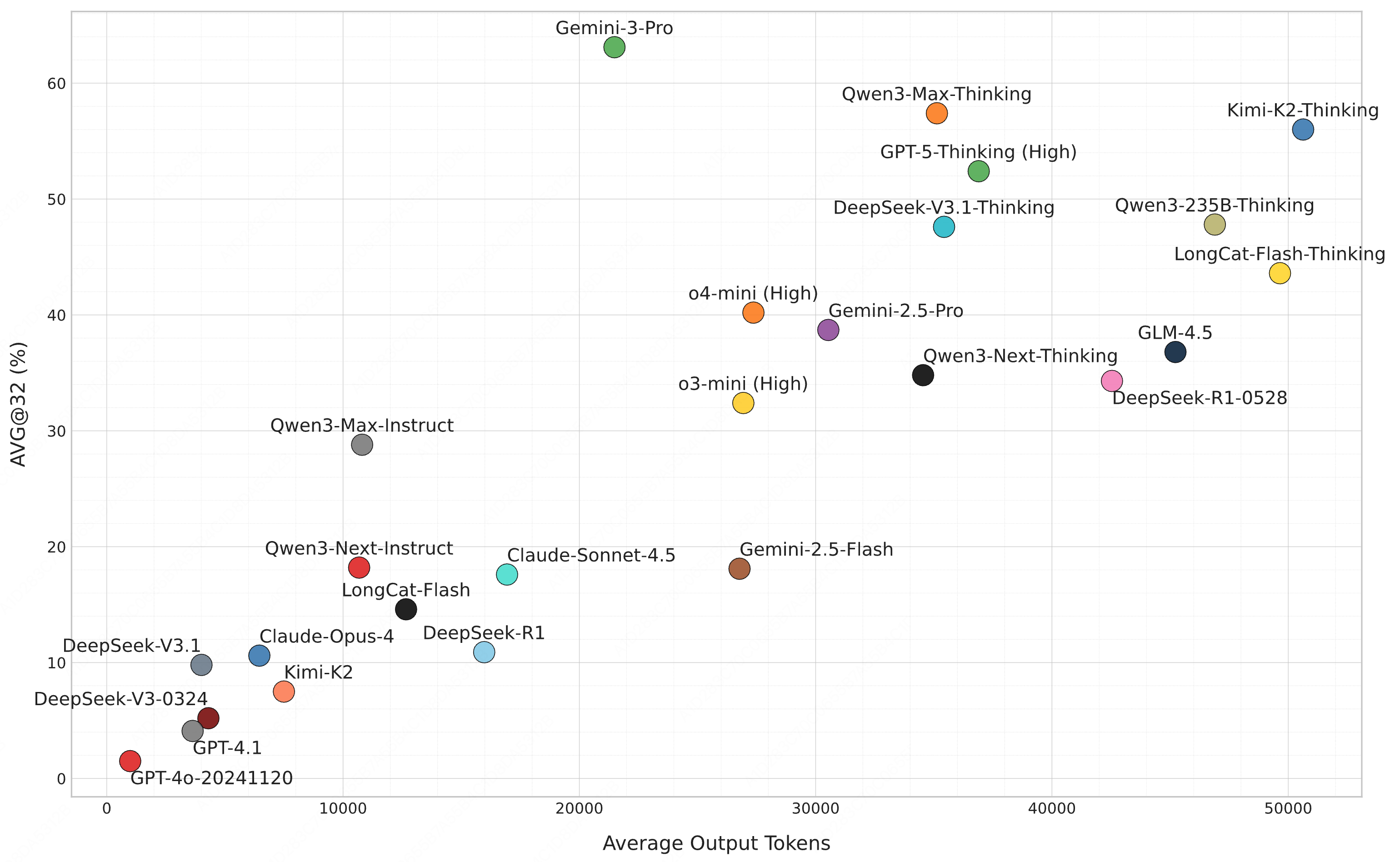
Token Efficiency

Sizes of model trees

Abstract

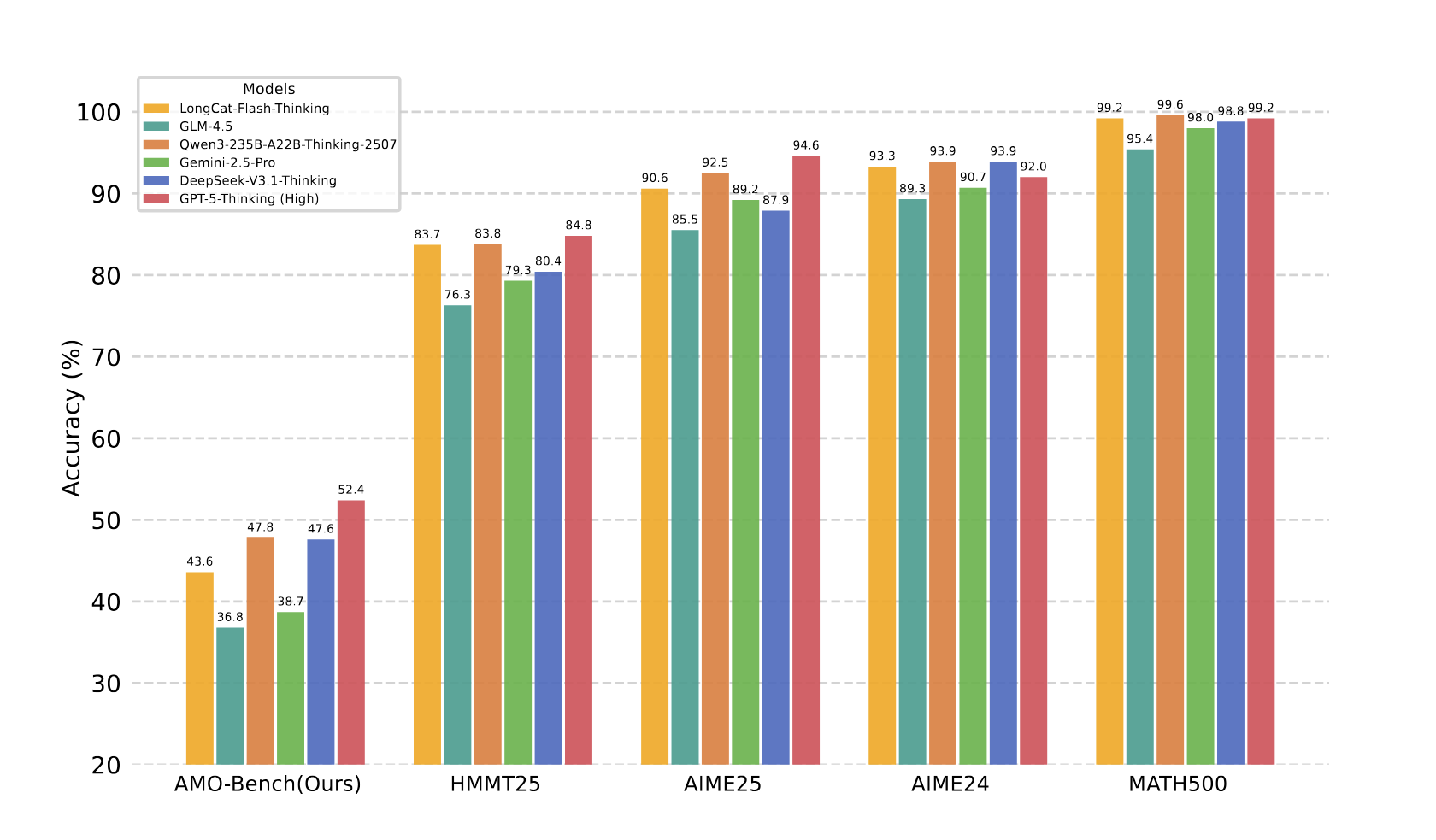
We present AMO-Bench, an Advanced Mathematical reasoning benchmark with Olympiad level or even higher difficulty, comprising 50 human-crafted problems. Existing benchmarks have widely leveraged high school math competitions for evaluating mathematical reasoning capabilities of large language models (LLMs). However, many existing math competitions are becoming less effective for assessing top-tier LLMs due to performance saturation (e.g., AIME24/25). To address this, AMO-Bench introduces more rigorous challenges by ensuring all 50 problems are (1) cross-validated by experts to meet at least the International Mathematical Olympiad (IMO) difficulty standards, and (2) entirely original problems to prevent potential performance leakages from data memorization. Moreover, each problem in AMO-Bench requires only a final answer rather than a proof, enabling automatic and robust grading for evaluation. Experimental results across 26 LLMs on AMO-Bench show that even the best-performing model achieves only 52.4% accuracy on AMO-Bench, with most LLMs scoring below 40%. Beyond these poor performances, our further analysis reveals a promising scaling trend with increasing test-time compute on AMO-Bench. These results highlight the significant room for improving the mathematical reasoning in current LLMs. We release AMO-Bench to facilitate further research into advancing the reasoning abilities of language models.

Directional Weight Score

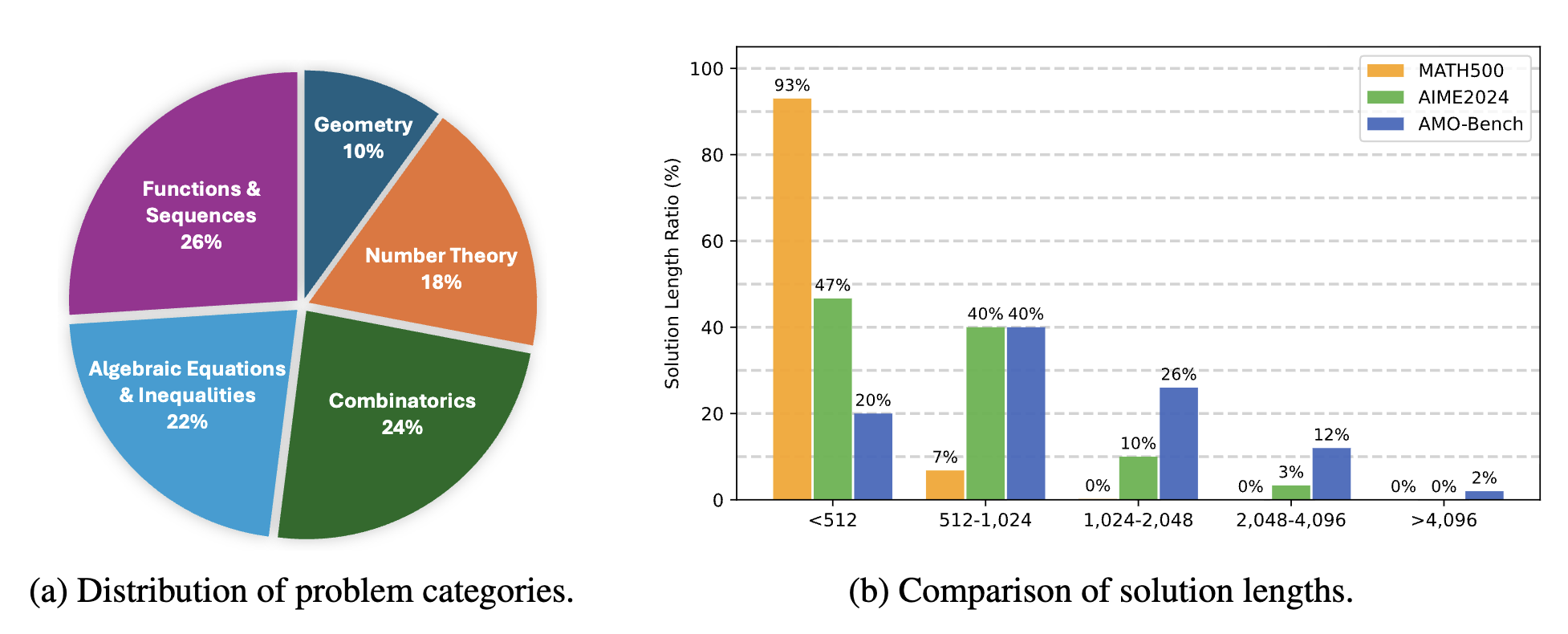
Dataset Statistics

A.Problem categories: Referring several official competition syllabus, we categorize the 50 problems of AMO-Bench into the following five primary categories: Algebraic Equations & Inequalities (11/50), Functions & Sequences (13/50), Geometry (5/50), Number Theory (9/50), and Combinatorics (12/50). Figure a show the overall distribution of problem categories in AMO-Bench.
B.Length distribution of human-annotated solutions: Since the problems in our AMO-Bench are equipped with manually annotated solutions, we can preliminarily analyze the reasoning complexity of these problems from the view of solution length. We measure solution length in terms of token count. Additionally, we compare the distribution of solution lengths with those from AIME24 and MATH500. Figure b illustrates the solution length distributions across these benchmarks. It reveals that solutions in AMO-Bench exhibit significantly higher lengths, indicating that problems in this benchmark are inherently more challenging and require more complex reasoning to arrive at the final answer.

Sizes of model trees

Construction and Grading Pipeline

A.Construction pipeline: AMO-Bench have built up a comprehensive multi-stage construction pipeline that covers the entire process from question creation to final inclusion. This pipeline comprises four major stages: (1) Data creation, all problems are independently designed by mathematics experts from top universities and educational institutions. Beyond the final answer, each problem author must provide a detailed step-by-step solution. (2) Quality review, each candidate problem undergoes blind review by at least three experts to assess its quality. (3) Originality review, the originality review stage aims to ensure that these newly created problems are not mere rewrites of publicly available materials, but demonstrate genuine originality. (4) Difficulty review, we implement a difficulty review stage to filter out problems lacking adequate complexity, to ensure that AMO-Bench presents a sufficient challenge to state-of-the-art LLMs.


B.Grading Pipeline: AMO-Bench employs different grading approaches based on the specific answer type for each problem. For problems requiring numerical, set, or variable-expression answers (39 out of 50), we employ the parser-based grading. For problems requiring descriptive answers (11 out of 50), we use LLM-based grading with o4-mini (Low) serving as the grading model.

Overview of the VitaBench construction pipeline

BibTeX

@misc{an2025amobench,
    title={AMO-Bench: Large Language Models Still Struggle in High School Math Competitions}, 
    author={Shengnan An and Xunliang Cai and Xuezhi Cao and Xiaoyu Li and Yehao Lin and Junlin Liu and Xinxuan Lv and Dan Ma and Xuanlin Wang and Ziwen Wang and Shuang Zhou},
    year={2025},
    eprint={2510.26768},
    archivePrefix={arXiv},
    primaryClass={cs.CL},
    url={https://arxiv.org/abs/2510.26768}
}